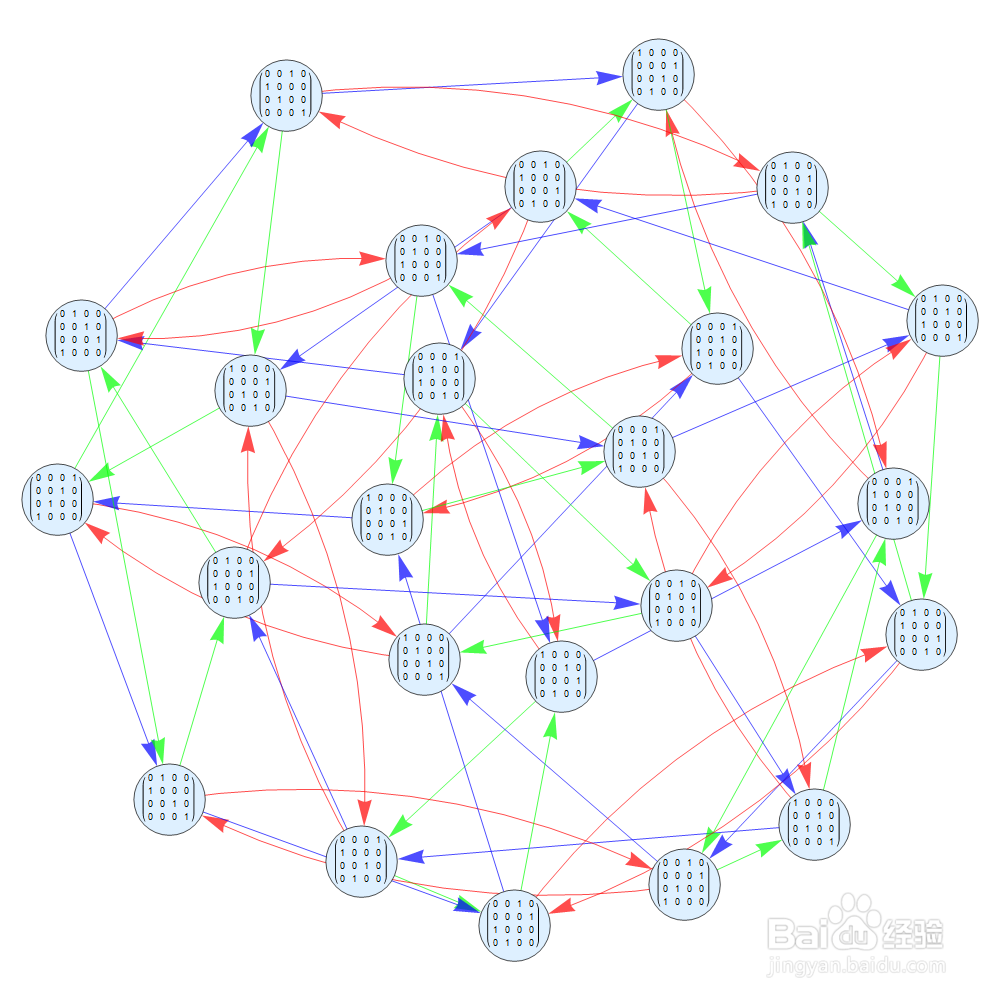
【抽象代数】给定集合生成的群的Cayley图
1、如果集合S含有三个元素:{{{0, 0巳呀屋饔, 0, 1}, {0, 1, 0, 0}, {0, 0, 1, 0}, {1, 0, 0, 0}},{{0, 0, 1, 0}, {0, 0, 0荑樊综鲶, 1}, {1, 0, 0, 0}, {0, 1, 0, 0}},{{0, 1, 0, 0}, {1, 0, 0, 0}, {0, 0, 0, 1}, {0, 0, 1, 0}}}
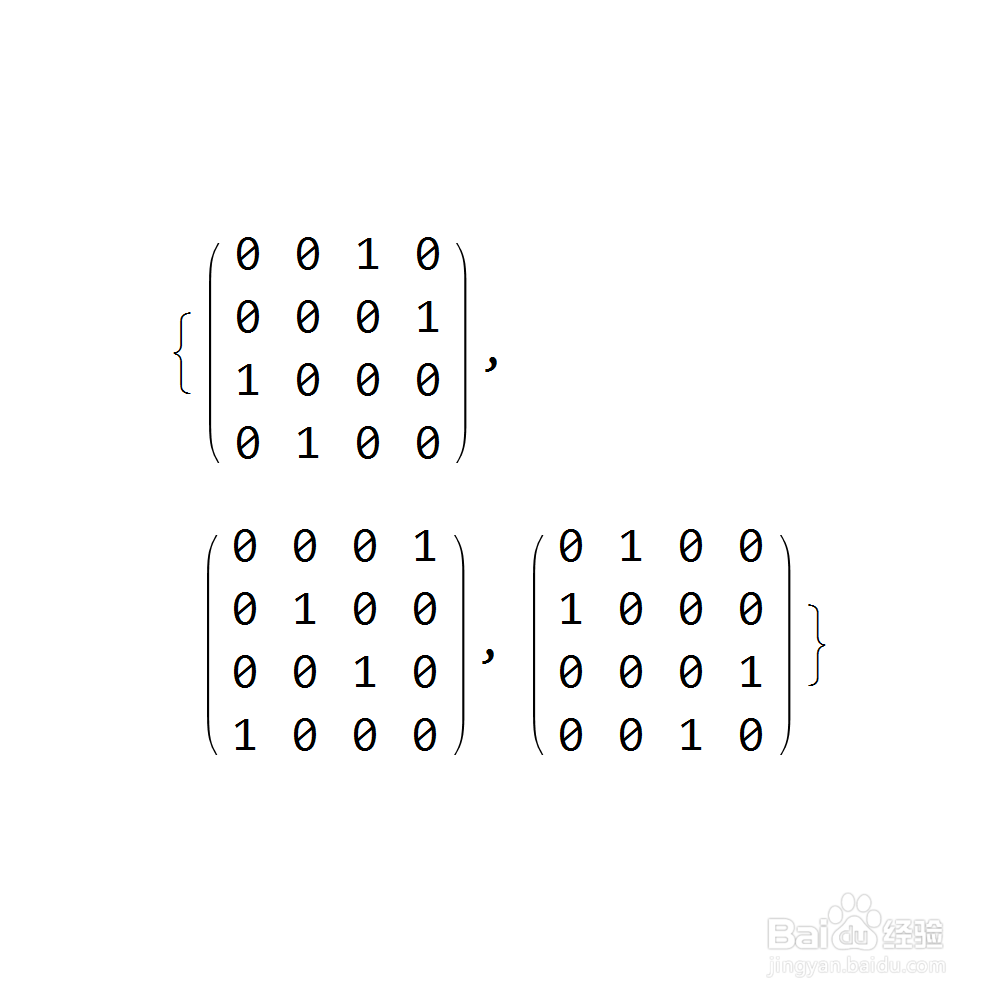
2、那么集合S就可以生成一个八阶群G,根据S来绘制G的Cayley图,如下:

3、S={{{0, 0, 0, 1}, {0, 0, 1, 0}, {0, 1, 0, 0}, {1, 0, 0, 0}}, {{0, 0, 0, 1}, {1, 0, 0, 0}, {0, 1, 0, 0}, {0, 0, 1, 0}}}生成的也是八阶群,但Cayley图与上图不太一样。

4、S={{{0, 0, 0, 1}, {0, 1, 0, 0}, {0, 0, 1, 0}, {1, 0, 0, 0}}, {{0, 1, 0, 0}, {0, 0, 0, 1}, {0, 0, 1, 0}, {1, 0, 0, 0}}}S的元素包括二阶元素一个、三阶元素一个,此时生成的群是六阶群。
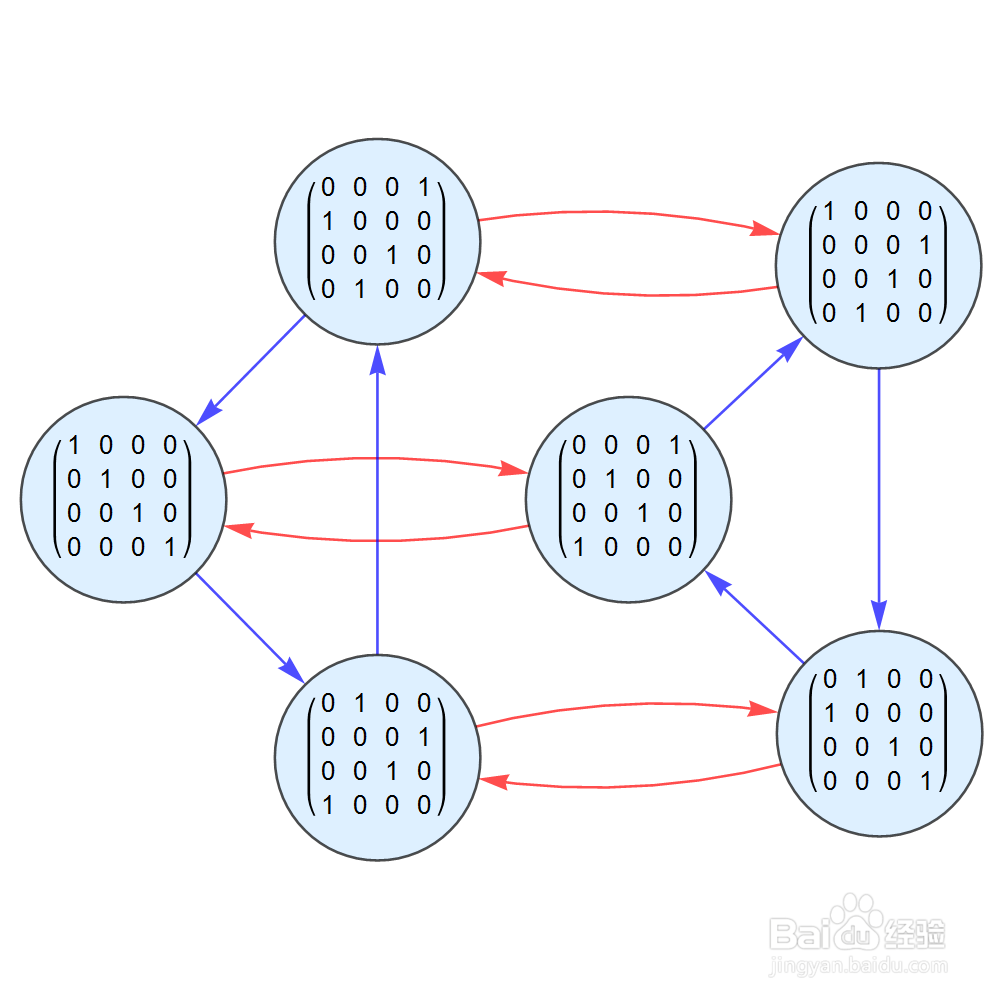
5、S={{{0, 0, 0, 1}, {0, 0, 1, 0}, {0, 1, 0, 0}, {1, 0, 0, 0}}, {{0, 0, 0, 1}, {0, 1, 0, 0}, {1, 0, 0, 0}, {0, 0, 1, 0}}}S的元素包括二阶元素一个、三阶元素一个,此时生成的群是十二阶群。它是s4的唯一的二阶子群,此时的Cayley图如下:
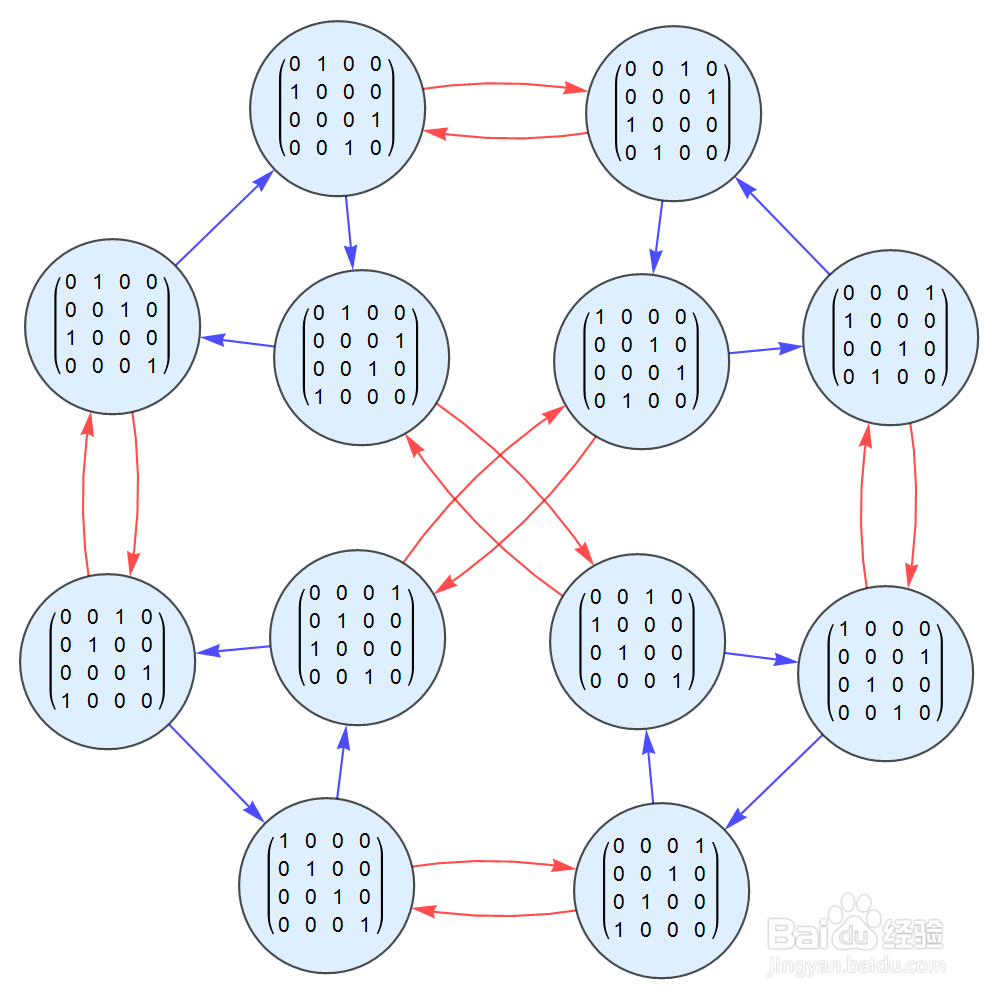
6、如果S等于:{{{0, 0, 0, 1娅势毁歹}, {0, 1, 0, 0}, {0, 0, 1, 0}, {1, 0, 0, 0}},{{0, 0, 1, 0}, {0, 0, 0, 1}, {1, 0, 0, 0}, {0, 1, 0, 0}},{{0, 0, 1, 0}, {0, 1, 0, 0}, {1, 0, 0, 0}, {0, 0, 0, 1}}}G是24阶群,恰好就是s4。但是因为几何S有3个元素,所以Cayley也有三种不同颜色的箭头。因为S中的元素都是二阶的,因此Cayley图中只有二阶轨道。这与下文中的s4的Cayley图不一样。
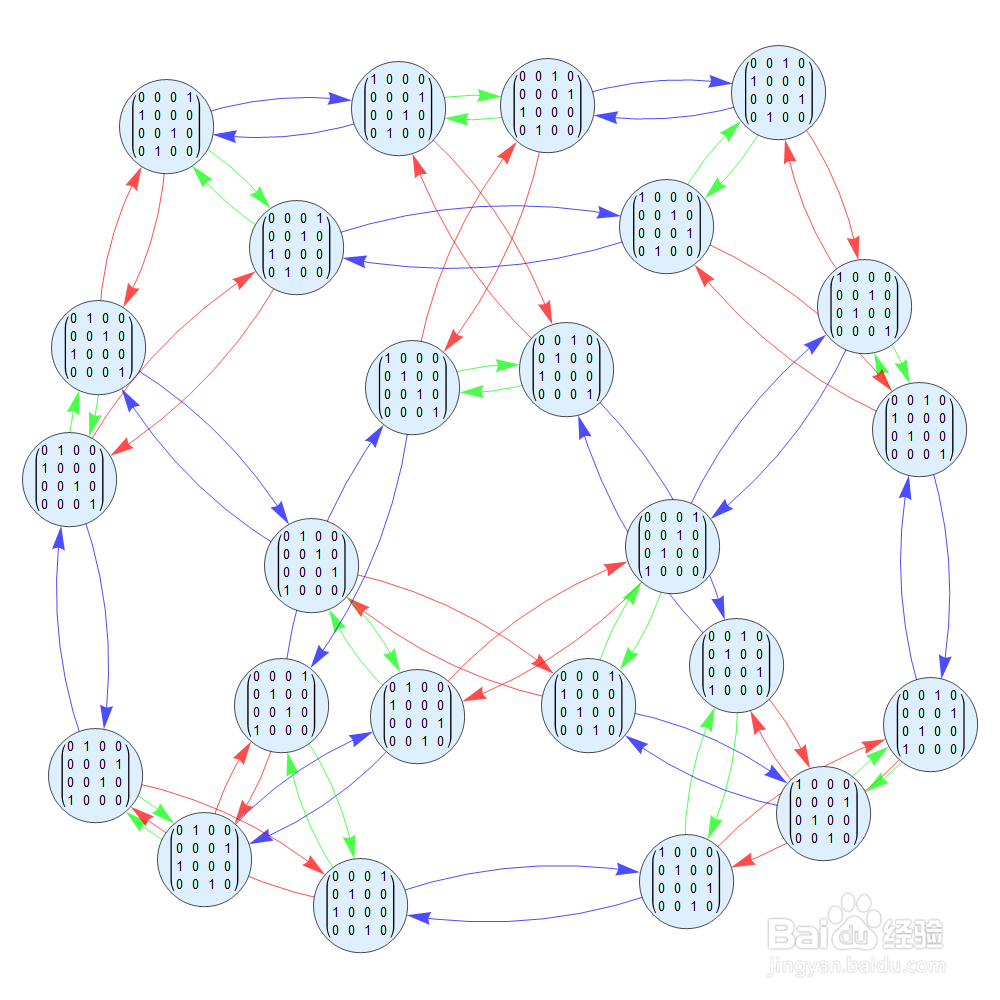
7、S={{{0, 0, 0, 1}, {0, 1, 0, 0}, {0, 0, 1, 0}, {1, 0, 0, 0}}, {{0, 1, 0, 0}, {0, 0, 1, 0}, {0, 0, 0, 1}, {1, 0, 0, 0}}}生成s4,但S的两个元素分别是二阶和四阶的,因此Cayley图中的轨道,分别是二阶和四阶的。

8、S={{{0, 0, 0, 1}, {0, 0, 1, 0}, {0, 1, 0, 0}, {1, 0, 0, 0}}, {{0, 0, 0, 1}, {0, 0, 1, 0}, {1, 0, 0, 0}, {0, 1, 0, 0}}, {{0, 0, 0, 1}, {0, 1, 0, 0}, {1, 0, 0, 0}, {0, 0, 1, 0}}}S中二阶、三阶、四阶元素各一个,请读者在Cayley图中找出所有的二阶、三阶、四阶轨道。